EJERCICIOS
6- Definición de número algebraico.
Cualquier número real que es solución de un polinomio no nulo con coeficientes racionales.
7- Demuestra que todo número racional es un número algebraico.
Todos los números racionales son algebraicos porque toda fracción de la forma a/b es solución de ax - b = 0 donde a y b son números reales.
8- Demuestra que todo número radical es algebraico.
Porque son soluciones de una ecuación algebraica. Ej:
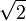es solución del polinomio: x2 - 2 = 0
9- Pon dos ejemplos de dos números algebraicos que no sean números radicales.
2x = 5 no es un número radical pero sí algebraico ya que su solución es 5/2.
x + 2 = o no es número radical, su solución es -2.
10- Pon tres ejemplos de números transcendentes.
Un número trascendente no es un número algebraico, pues no es solución de ninguna ecuación algebraica con coeficientes racionales. Es lo contrario a los números algebraicos.
- Número e
- Número π (pi)
donde 
es algebraico y b es algebraico pero irracional. Ejemplo: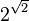 
Expresión algebraica que constituye la suma o la resta ordenadas de
un número finito de términos o monomios.
12- El polinomio nulo.
Aquel que todos sus coeficientes son 0. P(x)= 0x + 0
18- Enuncia el teorema del factor y aplícalo en el polinomio.
El teorema del factor dice que todo polinomio P(x) es divisible entre un polinomio de la forma x-a si solo si P(a) es = 0. (si a es una raíz de dicho polinomio).
36-
En la próxima entrada publicaré la continuación del examen.
No hay comentarios:
Publicar un comentario