- Dominio. Dom f
- Cortes con los ejes
- Continuidad y asíntotas (verticales, horizontales u oblicuas)
- Monotonía y extremos relativos de f mediante los signos y ceros de f´
- Convexidad y puntos de inflexión de f mediante signos y ceros de f´´
- La gráfica
- Otras... (recorrido, inyectividad, periodicidad...)
Aquí os traigo un par de ejemplos de como hallar la gráfica de cualquier función a partir de su ecuación. (iremos resolviendo de funciones sencillas a más complejas)
Ejemplo 1:
Estudio completo de la función definida por:
1- DOMINIO: Dom f = ℝ (por ser polinómica)
2- CORTES CON LOS EJES:
f(0) = 1 P(0,1)
f(x) = 0 resolvemos la ecuación a través del método de bisección.
P (-1,87 , 0)
3- CONTINUIDAD Y ASÍNTOTAS
Es continua por ser polinómica.
No hay asíntotas
4- MONOTONÍA Y EXTREMOS RELATIVOS
Estudiando los signos y ceros de la derivada.
5- CONVEXIDAD Y PUNTOS DE INFLEXIÓN
Estudiando los signos y ceros de la derivada segunda.
6- LA GRÁFICA
Mientras hemos estudiado las características está bien ir haciendo una tabla de valores de los puntos que obtenemos para después dibujar la gráfica.
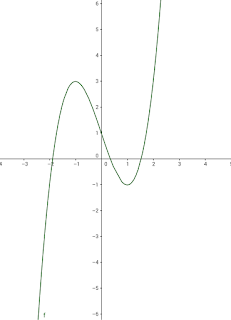
Ejemplo 2:
Estudio completo de la función definida por:
1- DOMINIO. Dom f = ℝ - (3/2)
2- CORTES CON LOS EJES.
f(0) = -1/3 P(0, -1/3)
f(x) = 0 x= -1 P(-1, 0)
3- CONTINUIDAD Y ASÍNTOTAS
Es continua en todo su dominio por ser racional, cociente de polinómicas.
Asíntota vertical en x = 3/2
Asíntota horizontal en y= 1/2
NO hay asíntotas oblicuas
4- MONOTONÍA Y EXTREMOS RELATIVOS
Estudiando los signos y ceros de la derivada.
5- CONVEXIDAD Y PUNTOS DE INFLEXIÓN
Estudiamos la segunda derivada
6- LA GRÁFICA
Primero tabla de valores con los datos conocidos
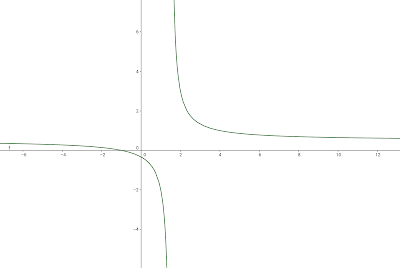











No hay comentarios:
Publicar un comentario