De una manera brusca y para que nos entendamos la derivada es la pendiente de la recta tangente (en un punto determinado).
Si nos referimos a funciones, una función es derivable cuando es derivable en todos los puntos de su dominio.

En la imagen se muestra que la derivada de la función en el punto marcado es equivalente a la pendiente de la recta tangente.
Derivada de una función en un punto.

Ejemplo:
Función derivada de las funciones elementales.
Función constante:


Función identidad:
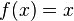

Función lineal:

Función afín:
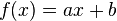

Función potencial:


Ejemplos:
Función polinómica:
Para resolverlas podemos entenderlas como suma de funciones más sencillas.
Ejemplo:
Función exponencial:


Caso especial:
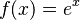

Función logarítmica:




FUNCIONES TRIGONOMÉTRICAS:
1- Funciones trigonométricas:
 |  |
 |  |
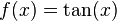 |  |
2- Funciones inversas de las trigonométricas:





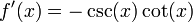
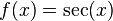





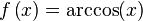











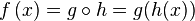



No hay comentarios:
Publicar un comentario