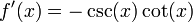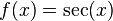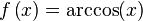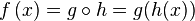Hoy os traigo otra reflexión, esta vez sobre un examen que hemos realizado recientemente (sobre derivadas e integrales), dentro de unos días cuando mi profesor me entregue el examen comentaré con vosotros cada uno de los ejercicios ya que ahora no recuerdo exactamente mis soluciones, pero en términos generales mi sensación al acabar el examen fue bastante positiva, no esperaba que pudiera hacer casi todos los ejercicios (excepto el ejercicio 3, que era un problema de optimización y a primera vista me pareció bastante difícil por lo que no le dediqué el suficiente tiempo pero al revisarlo en casa me dí cuenta que era más sencillo de lo pensaba, pero bueno en otra entrada comentaremos los ejercicios) me di cuenta que tenía más idea sobre los temas de lo que pensaba aunque debo de añadir que mi profesor se portó bastante bien al poner el examen y confieso que tenía una chuleta con todas las fórmulas ya que no veo el sentido de aprenderte 50 fórmulas de memoria, pienso que lo importante es saber resolver los ejercicios, entender los conceptos y saber aplicar dichas fómulas (por muchas fórmulas que tengas si no las entiendes no sirven de nada) así que desde aquí lanzo un llamamiento a todos los profesores de matemáticas para decirlos que las fórmulas deberían de ser una herramienta más en los exámenes al igual que una calculadora.
Por otra parte creo que mi parte favorita del examen de matemáticas es el ambiente que se crea en clase cuando lo realizamos, los nervios se quedan en casa (al contrario que en el resto de asignaturas) incluso hasta nos divertimos! quién me diría que me divertiría haciendo un examen de matemáticas en primero de bachillerato, creo que poco a poco entiendo la asignatura y lo que me sorprendía al principio de curso ahora lo veo normal e incluso en muchos aspectos mejor que la enseñanza tradicional.
Ahora podría valorar mi examen con una nota y hacer la tipica reflexión de los exámenes, pero no lo voy a hacer ya que me quedo con la sensación de que sé los conceptos principales de estos temas y al final eso es lo importante, aprender, independientemente de una nota y ahora a seguir trabajando hasta el global!
Blog de Ana Pardo
La vida en númer0s
BIENVENIDOS Este blog va dirigido a todas aquellas personas enamoradas de las matemáticas o a quienes les cuesta enterderlas, en él os contaré mi experiencia con ellas en 1º de bach. Espero que os sirva de ayuda. 'Si la gente no piensa que las matemáticas son simples, es solo porque no se dan cuenta de lo complicada que es la vida.' John Von Neumann
sábado, 11 de junio de 2016
lunes, 30 de mayo de 2016
Aplicaciones de las derivadas al estudio completo de una función
Antes de nada, ¿qué hay que estudiar cuando me piden el estudio completo de una función?
Aquí os traigo un par de ejemplos de como hallar la gráfica de cualquier función a partir de su ecuación. (iremos resolviendo de funciones sencillas a más complejas)
Ejemplo 1:
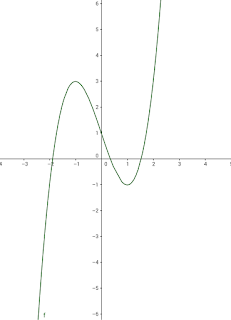
Estudio completo de la función definida por:
1- DOMINIO: Dom f = ℝ (por ser polinómica)
2- CORTES CON LOS EJES:
f(0) = 1 P(0,1)
f(x) = 0 resolvemos la ecuación a través del método de bisección.
P (-1,87 , 0)
3- CONTINUIDAD Y ASÍNTOTAS
Es continua por ser polinómica.
No hay asíntotas
4- MONOTONÍA Y EXTREMOS RELATIVOS
Estudiando los signos y ceros de la derivada.
5- CONVEXIDAD Y PUNTOS DE INFLEXIÓN
Estudiando los signos y ceros de la derivada segunda.
6- LA GRÁFICA
Mientras hemos estudiado las características está bien ir haciendo una tabla de valores de los puntos que obtenemos para después dibujar la gráfica.
Ejemplo 2:
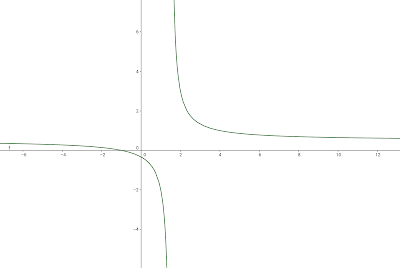
Estudio completo de la función definida por:
1- DOMINIO. Dom f = ℝ - (3/2)
2- CORTES CON LOS EJES.
f(0) = -1/3 P(0, -1/3)
f(x) = 0 x= -1 P(-1, 0)
3- CONTINUIDAD Y ASÍNTOTAS
Es continua en todo su dominio por ser racional, cociente de polinómicas.
Asíntota vertical en x = 3/2
Asíntota horizontal en y= 1/2
NO hay asíntotas oblicuas
4- MONOTONÍA Y EXTREMOS RELATIVOS
Estudiando los signos y ceros de la derivada.
5- CONVEXIDAD Y PUNTOS DE INFLEXIÓN
Estudiamos la segunda derivada
6- LA GRÁFICA
Primero tabla de valores con los datos conocidos
- Dominio. Dom f
- Cortes con los ejes
- Continuidad y asíntotas (verticales, horizontales u oblicuas)
- Monotonía y extremos relativos de f mediante los signos y ceros de f´
- Convexidad y puntos de inflexión de f mediante signos y ceros de f´´
- La gráfica
- Otras... (recorrido, inyectividad, periodicidad...)
Aquí os traigo un par de ejemplos de como hallar la gráfica de cualquier función a partir de su ecuación. (iremos resolviendo de funciones sencillas a más complejas)
Ejemplo 1:
Estudio completo de la función definida por:
1- DOMINIO: Dom f = ℝ (por ser polinómica)
2- CORTES CON LOS EJES:
f(0) = 1 P(0,1)
f(x) = 0 resolvemos la ecuación a través del método de bisección.
P (-1,87 , 0)
3- CONTINUIDAD Y ASÍNTOTAS
Es continua por ser polinómica.
No hay asíntotas
4- MONOTONÍA Y EXTREMOS RELATIVOS
Estudiando los signos y ceros de la derivada.
5- CONVEXIDAD Y PUNTOS DE INFLEXIÓN
Estudiando los signos y ceros de la derivada segunda.
6- LA GRÁFICA
Mientras hemos estudiado las características está bien ir haciendo una tabla de valores de los puntos que obtenemos para después dibujar la gráfica.

Ejemplo 2:
Estudio completo de la función definida por:
1- DOMINIO. Dom f = ℝ - (3/2)
2- CORTES CON LOS EJES.
f(0) = -1/3 P(0, -1/3)
f(x) = 0 x= -1 P(-1, 0)
3- CONTINUIDAD Y ASÍNTOTAS
Es continua en todo su dominio por ser racional, cociente de polinómicas.
Asíntota vertical en x = 3/2
Asíntota horizontal en y= 1/2
NO hay asíntotas oblicuas
4- MONOTONÍA Y EXTREMOS RELATIVOS
Estudiando los signos y ceros de la derivada.
5- CONVEXIDAD Y PUNTOS DE INFLEXIÓN
Estudiamos la segunda derivada
6- LA GRÁFICA
Primero tabla de valores con los datos conocidos

sábado, 28 de mayo de 2016
Entrevista a Luis María Abia Llera
Hace bastante tiempo compartí con vosotros una posible entrevista para realizar al matemático Luis Abia (si quieres recordar dicha entrevista Pinche aquí)
Pues bien por fin mis compañeros y yo hemos recibido sus respuestas y me gustaría comentar con vosotros aquellos aspectos de la entrevista que más me han gustado.
Antes de nada agradezco a Luis su tiempo y empeño en responder a las preguntas.
Lo primero que me ha llamado la atención es la cercanía y sinceridad con la que ha respondido y nos ha ayudado a conocerle un poquito más:
Se decantó por las matemáticas porque se le daban bastante bien y porque ganó una beca al quedar tercero en una Olimpiada matemática y eso le impulsó finalmente a estudiar esta disciplina. Su motivación diaria son sus alumnos, la enseñanza y su mayor satisfacción resolver un problema al que ha dedicado días y días.Afirma que las matemáticas están presentes en nuestro día a día y que es impensable un mundo sin ellas, de hecho el futuro estará marcado por las nuevas tecnologías, por la informática, ciencia que va de la mano con su querida disciplina. Aunque él reivindica que se aprende trabajando con lapiz, papel y resolviendo problemas y problemas.Nos aconseja que lo más importante a la hora de empezar una carrera es la actitud.Las matemáticas es una de las asignaturas más odiadas por los estudiantes, nuestro entrevistado nos explica que la causa de este fracaso es que estamos ante una asignatura acumulativa (que no te puedes preparar el día antes del examen), una asignatura que hay que trabajar día a día y ser constante con dicha práctica. Por último respondió a la pregunta que yo le plantee sobre la eliminación de la filosofía como asignatura obligatoria y me gusta que por mucho matemático que sea sepa admitir la importancia de dicha asignatura, y sorprendiéndome Luis Abia se decanta por la filosofía.
En conclusión, puede que lleve muchos años dedicados a las matemáticas pero aún sigue teniendo la curiosidad del primer día, aún se sorprende con lo amplia y maravillosa que es esta ciencia infinita.
Tras su entrevista podría definir las cualidades de un gran matemático: motivación, curiosidad y perseverancia.
El mundo necesita más gente que ame lo que hace y Luis María Abia Llera ama las matemáticas.
domingo, 15 de mayo de 2016
Examen derivabilidad. (Ejercicios del 7 al 9)
7-
8-
9-
En los ejercicios 6 y 10 me han surgido unas pequeñas dudas que espero resolver mañana en clase, y poder ya compartir el examen al completo.
8-
9-
En los ejercicios 6 y 10 me han surgido unas pequeñas dudas que espero resolver mañana en clase, y poder ya compartir el examen al completo.
Transmisión del conocimiento: Difusión científica
Índice
1. Introducción
2. Resumen y palabras clave
3. Importancia de la difusión científica.
- Prehistoria:
1. Introducción
2. Resumen y palabras clave
3. Importancia de la difusión científica.
- Sociedades científicas
- Prehistoria:
- Símbolos.
- Sonidos. Palabras. Lenguaje.
- Historia:
- LA ESCRITURA (libros, manuscritos)
- La música
- Culturas clásicas (Grecia y Roma)
- Monasterios
- Imprenta
- Universidades
- Las TIC
5. Conclusión.
6. Bibliografía
martes, 10 de mayo de 2016
LA DERIVADA
Antes de empezar a hablar mil cosas sobre las derivadas dejemos claro ¿Qué es una derivada?
De una manera brusca y para que nos entendamos la derivada es la pendiente de la recta tangente (en un punto determinado).
Si nos referimos a funciones, una función es derivable cuando es derivable en todos los puntos de su dominio.

En la imagen se muestra que la derivada de la función en el punto marcado es equivalente a la pendiente de la recta tangente.
Derivada de una función en un punto.

Ejemplo:

Función derivada de las funciones elementales.
Función constante:


Función identidad:
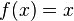

Función lineal:

Función afín:
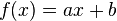

Función potencial:


Ejemplos:
Función polinómica:
Para resolverlas podemos entenderlas como suma de funciones más sencillas.
Ejemplo:
Función exponencial:


Caso especial:
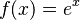

Función logarítmica:




FUNCIONES TRIGONOMÉTRICAS:
1- Funciones trigonométricas:
2- Funciones inversas de las trigonométricas:
De una manera brusca y para que nos entendamos la derivada es la pendiente de la recta tangente (en un punto determinado).
Si nos referimos a funciones, una función es derivable cuando es derivable en todos los puntos de su dominio.

En la imagen se muestra que la derivada de la función en el punto marcado es equivalente a la pendiente de la recta tangente.
Derivada de una función en un punto.

Ejemplo:
Función derivada de las funciones elementales.
Función constante:


Función identidad:
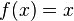

Función lineal:

Función afín:
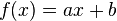

Función potencial:


Ejemplos:
Función polinómica:
Para resolverlas podemos entenderlas como suma de funciones más sencillas.
Ejemplo:
Función exponencial:


Caso especial:
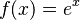

Función logarítmica:




FUNCIONES TRIGONOMÉTRICAS:
1- Funciones trigonométricas:
 |  |
 |  |
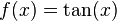 |  |
2- Funciones inversas de las trigonométricas:
Suscribirse a:
Entradas (Atom)