Para comprender bien el concepto tenemos que recurrir a la teoría de conjuntos con un diagrama de Venn.
Cada flecha representa una pareja de un elemento de A con uno de B ---> Producto cartesiano.
Parejas ordenadas de A y B, AxB: este conjunto tiene 12 elementos ( 3 elementos de A x 4 elementos de B).
Pero realmente no vemos todo el conjunto AxB únicamente vemos 4 parejas (recordad que cada flecha es una pareja), vemos una parte del conjunto AxB, un subconjunto del producto cartesiano de A y B que se llama correspondencia de A y B.
Al conjunto A lo llamaremos conjunto inicial y al conjunto B conjunto final dentro de los cuales encontramos los subconjuntos original e imagen respectivamente.
Aparte del diagrama de Venn tenemos otras dos formas de representar una correspondencia:
Definición por extensión:
Describirla a través de todos sus elementos. (en forma de conjunto)
C= la correspondencia
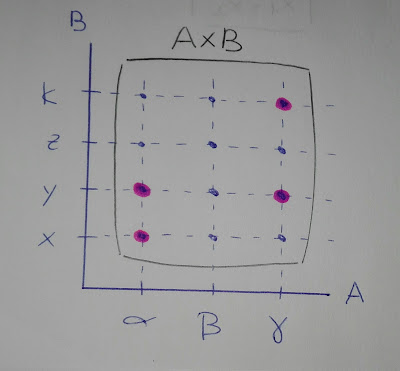
Diagrama lineal:
Un conjunto (en este caso A) sobre una recta horizontal y el otro (B) en una recta vertical.
Cada intersección de ambos conjuntos (cada punto) sería una posible pareja y los puntos más marcados sería los de la correspondencia que nos interesa.
Aplicación
Una aplicación es un tipo de correspondencia en la que todos los elementos del conjunto inicial están emparejados una o ninguna vez con algún elemento del conjunto final. (la anterior correspondencia AxB no sería una aplicación.)
- Aplicación inyectiva: es una aplicación en la que todos los elementos del conjunto final están emparejados 1 o ninguna vez.
- Sucesión: aplicación ℕ--> ℝ.
- Función: aplicación ℝ --> ℝ.
Función seno: y= f(x)= sen (x)
Esta función NO es inyectiva, ya que varios elementos del conjunto final (eje y) estan emparejados más de 1 vez.
Función arcoseno ("dar la vuelta al seno"): no sería aplicación porque la función seno no es inyectiva así que para que sea una aplicación debemos restringir esta función a un intervalo (Función restringida). Por ejemplo el intervalo:








No hay comentarios:
Publicar un comentario