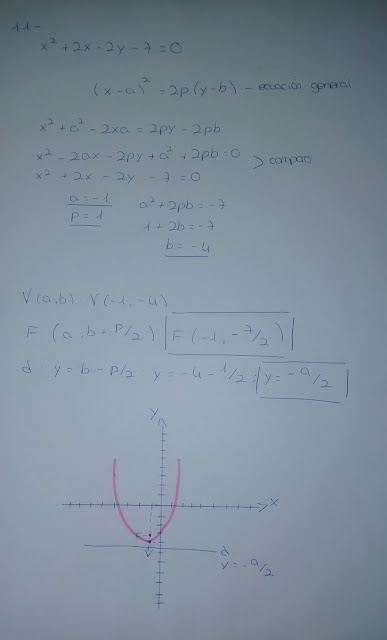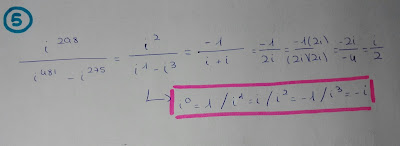Examen para casa. Temas 6, 7 y 8 (Parte 2)

9-

a) Posición relativa de las rectas r: 3x - y + 1 = 0 y s: 3x + y +1 = 0.

b) Halla un punto del plano que equidiste de las rectas r y s.

10-

Dibuja el  lugar geométrico de los puntos del plano cuyas sumas de distancias a los puntos fijos F₁(8,0) y F₂(-8,0) son siempre iguales a 20 unidades. ¿Es una cónica? En caso afirmativo, ¿qué tipo de cónica es y cuál es su excentricidad?

11-

a) Halla el foco y la directriz de la parábola cuya ecuación es x² + 2x – 2y – 7 = 0. Su vértice no es el origen de coordenadas. 

Ayuda: Expresa la ecuación en la forma (x – h)² = 2p(y – k) (ecuación reducida de la parábola) è Las coordenadas del vértice V(h,k)

b) Dibuja la parábola y todos sus elementos.

12-

a) Definición: lado recto de una cónica es una cuerda focal (segmento cuyos extremos son 

puntos de la cónica y que pasa por el foco) perpendicular al eje focal. Demuestra que la 

longitud l del lado recto de una hipérbola es l= 2b²/a

b) Halla la ecuación de una hipérbola de centro O, el origen de coordenadas, de eje focal el eje de abcisas, de longitud de lado recto 6 unidades y de excentricidad √7 /2.

Examen para casa. Temas 6,7 y 8 (Parte 1)

1- 

 a) ¿Las funciones reales de variable real cuyas expresiones algebraicas son x² y x³ son inyectivas?

Una función es inyectiva si no hay dos elementos que tengan imágenes iguales así que la 

función f(x) = x² no es inyectiva porque por ejemplo la imagen f(x)= 9 se puede obtener como 

f = 3/ f= -3. 

En cambio, la función f(x) = x³ sí es inyectiva ya que a cada valor de x le corresponde una 

imagen f(x) diferente.

 b) ¿La raíz cuadrada y la raíz cúbica de un número real son operaciones?

No, son números complejos. 

 c) ¿La raíz cuadrada y la raíz cúbica de un número complejo son operaciones?

Sí, porque se pueden obtener como la inversa de las respectivas funciones. f(z) = z²   / f(z) = z³

d) Calcula y dibuja el resultado.

2- 

Utiliza la fórmula de Moivre para demostrar las siguientes igualdades trigonométricas:

Y encuentra las correspondientes fórmulas para sen3x y cos3x.

3- 

Halla el módulo y el argumento del inverso de un número complejo z distinto de 0.

5- 

Sean los vectores de V₂ u (1,-1) y v (-2,0).

 a) ¿El sistema (u.v) es una base de V₂?

Sí, es una base porque son dos vectores no nulos con distinta dirección.

 b) Expresa el vector w (a.b) como combinación lineal de los vectores u y v.

c) Encuentra un vector proporcional a v cuyo modulo sea √2.

vector proporcional = (√2 , 0) o (-√2 ,0)

 d) Halla el vector proyección de u sobre v. ¿Es unitario? Halla un vector unitario con la misa

 dirección que dicho vector proyección.

6- 

a) Definición de baricentro de un triángulo: coordenadas.

b) Haz de rectas que pasan por un punto: definición y ecuación.

c) Interpretación geométrica de las transformaciones elementales sobre un sistema compatible y determinado de dos ecuaciones lineales con dos incógnitas.

d) Demuestra que el lugar geométrico de los puntos del plano que equidistan de dos rectas secantes es el conjunto de puntos de las dos bisectrices de los “ángulos” formados por dichas rectas.

8- 

 Dadas las rectas r=y=3x+1 y s=y=-3x-1. Halla:

 a) Todas las ecuaciones de las rectas r y s.

 b) La pendiente de las rectas r y s. ¿Son perpendiculares?

No, porque sus vectores no son ortogonales. u (1.3) y v (1,-3)

 c) El ángulo formado por dichas rectas.

Dibuja las rectas r y s y todos los elementos aparecidos en los apartados anteriores.

Ejercicios de NÚMEROS COMPLEJOS

Para rematar este tema de los números complejos os dejo algunos ejercicios del tema, aquellos que me han parecido los más interesantes.

18- La suma de dos números complejos es 5 - 3i. Su cociente es imaginario puro y la parte real del numerador es 4. Halla dichos números.